Numerous of different phenomena around us can be described by network models. In many cases it is a natural choice, because one can clearly distinguish vertices and edges in the structure of the system. This approach is applied in a wide range of problems. The complex structures studied by physicists, biologists, economists and sociologists, as well as phenomena occurring on the border of these sciences can be captured using graph theory. The flexibility is so high thanks to an arbitrary interpretation of vertices and connections. In physics it may be atoms, in biology neurons, in economics financial institutions and in sociology people or social groups. Assuming two-body interactions, the limitation is the discrete nature of the phenomenon, but only in the structure, because the connections can be weighted to indicate for example the distance between cities, or the strength of the interaction, and vertices can be described by any state determining for instance the energy or opinion. In recent times, a great deal of effort has been devoted to analyzing social networks, examining the dynamics of opinion or culture, the spread of epidemic, information or innovation etc.
In this project we study the model of dissemination of culture originally defined by political scientist Rober Axelrod. The purpose of this model is to describe global behavior of multicultural society by simple local dynamics. In first attempt only square lattice as the structure of interactions was considered. But real topology of social networks is different. Usually we can observe high values of clustering coefficient and power-law degree distribution. Keeping this in mind, we try to extend previous approaches to the problem and analyze the influence of the topology on the behavior of the system.
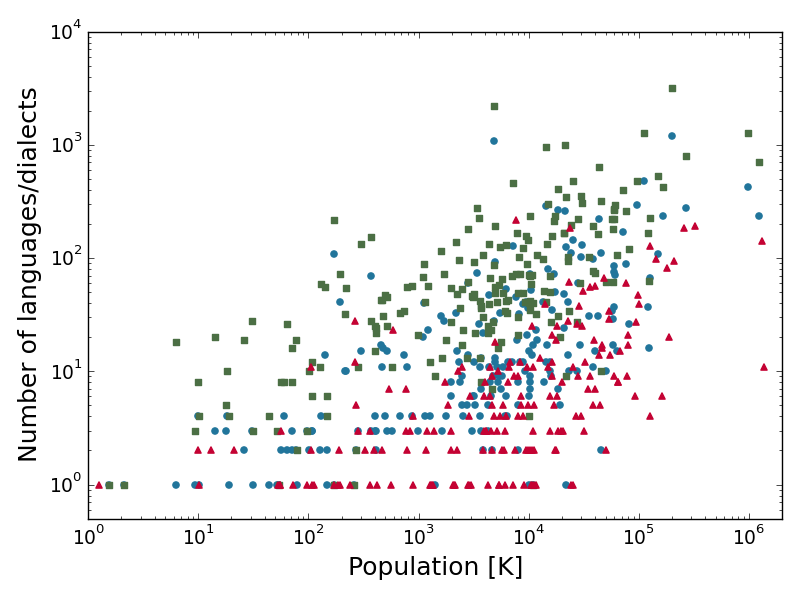
In second part of this project we consider different interpretation of Axelrod model. It can be seen as a model describing language change in society. Despite the fact it manages to capture the essence of social interactions, its interpretation considering languages was abandoned after very first publication, due to the contradiction with the empirical data. Anthropological study of Solomon Islands in the late 70’s showed that the number of languages functioning on an island grows with the size of the island. As noted in the original paper, results of the first model defined on a static square lattice were exactly opposite – the number of domains was decreasing with increasing size of the lattice. Moreover, the first adaptive model, taking into account coevolution of the nodes’ states and the topology of the network, did not solve this issue. We proposed modification that can fix this problem and produce results qualitatively in agreement with empirical data.
In this project we study the model of dissemination of culture originally defined by political scientist Rober Axelrod. The purpose of this model is to describe global behavior of multicultural society by simple local dynamics. In first attempt only square lattice as the structure of interactions was considered. But real topology of social networks is different. Usually we can observe high values of clustering coefficient and power-law degree distribution. Keeping this in mind, we try to extend previous approaches to the problem and analyze the influence of the topology on the behavior of the system.
In second part of this project we consider different interpretation of Axelrod model. It can be seen as a model describing language change in society. Despite the fact it manages to capture the essence of social interactions, its interpretation considering languages was abandoned after very first publication, due to the contradiction with the empirical data. Anthropological study of Solomon Islands in the late 70’s showed that the number of languages functioning on an island grows with the size of the island. As noted in the original paper, results of the first model defined on a static square lattice were exactly opposite – the number of domains was decreasing with increasing size of the lattice. Moreover, the first adaptive model, taking into account coevolution of the nodes’ states and the topology of the network, did not solve this issue. We proposed modification that can fix this problem and produce results qualitatively in agreement with empirical data.